참고
Efficient and robust approximate nearest neighbor search using HNSW 논문
C++ HNSW implementation with python bindings
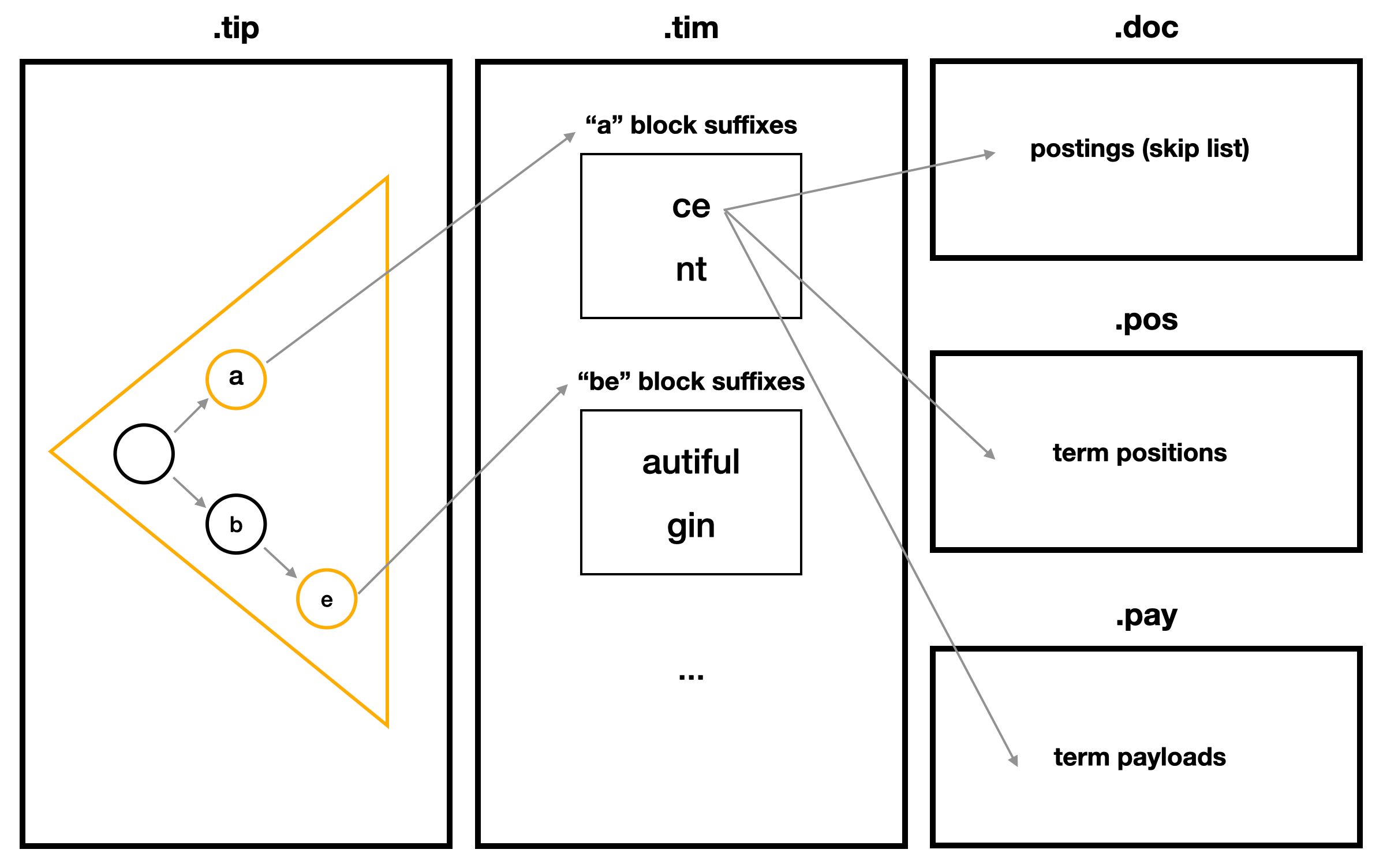
Lucene95HnswVectorsFormat code
배경
ANN(Approximate Nearest Neighbor)이란 공간에서 query 벡터와 유사한 벡터(문서, 이미지 등이 학습된 데이터)들을 빠르게 검색하는 알고리즘 이다. Approximate라 표현하는 이유는 ANN이 반환한 벡터들이 실제 정답셋이 아니다. 벡터 크기가 보통 1000차원 이상 크고 학습하는 데이터도 규모있는 서비스 경우 수 억건이 넘어가기에 실제 정답을 구하는 비용이 크다. 효율적으로 계산하기 위해 recall(재현율) 및 precision(정밀도)를 기준치 이상 유지하며 빠르게 검색하는 알고리즘들이 개발되고 있다.
(http://ann-benchmarks.com/ 참고)
이번 글은 ANN 알고리즘 중 HNSW에 대해 알아보자. HNSW는 본래 c++ 기반으로 위 참고 github에서 먼저 공개되었고 Lucene9x, ES8x 부터 적용되었다. Lucene에서는 native java로 변환하여 적용되었으며 SIMD 등 칩에 최적화하는 과정이 빠져있어 c++보다 성능이 떨어질 수 있다. 참고로 현재 recall 대비 가장 빠른 검색 성능을 내는 알고리즘은 2020년 구글이 공개한 ScaNN 이다.
분석
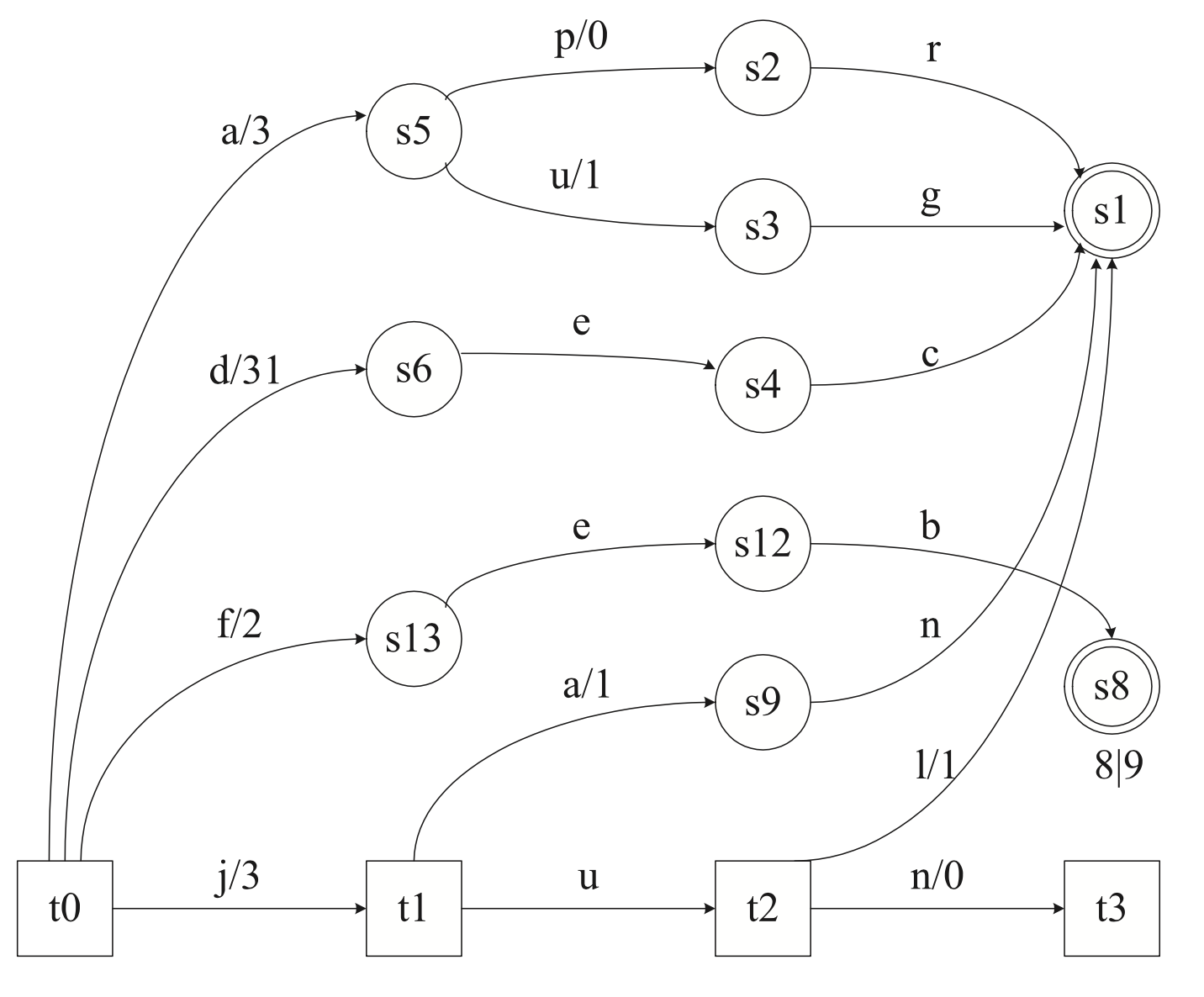
1. NSW
NSW는 공간상의 벡터들을 배치하고 이들을 적절하게 연결하여 벡터 간 탐색 가능하도록 만드는 알고리즘이다. 크게 벡터를 저장하는 방식(Dense, Sparse ...), 거리 함수, 그리고 벡터를 연결하는 알고리즘(방향성 그래프 기반)으로 구성한다.

그림1 은 편의상 2차원 공간에 4개의 벡터들로 NSW를 구성한 예시이다. M은 이웃 수를 나타내며 보통 10 ~ 20개로 구성한다. 제한된 이웃 수로 효율적인 NSW를 구성하기 위해 아래 두 가지 목표를 설정한다.
1. 최소 방문으로 원하는 목적지 탐색
2. 탐색 불가능한 노드가 없도록
1번은 NSW 내 임의의 두 벡터를 선택했을 때 최단경로 길이의 평균을 최소화 하는 것이다. 2번은 edge(이웃)가 방향성을 가지기 때문에 발생하는 탐색불가능 노드를 최소화 하는 것이다. 예를들어 아래와 같은 상황을 만들면 ANN 성능이 크게 떨어진다.

SELECT-NEIGHBORS-SIMPLE(q,C,M)
Input: base element q,
candidate elements C,
number of neighbors to return M
Output: M nearest elements to q
return M nearest elements from C to q
그림2 는 가장 가까운 벡터들로만 이웃을 구성했을 때 NSW 예시이다. 왼쪽 3개의 벡터들은 서로 연결되어 탐색 가능하지만 오른쪽위 벡터로 가는 길은 없다. HNSW 논문의 Algorithm 3(SELECT-NEIGHBORS-SIMPLE)은 단순 거리계산만 적용된 이웃탐색 알고리즘이며 사용하지 말라고 알려주는 것이다. 이를 대신하여 Algorithm 4(SELECT-NEIGHBORS-HEURISTIC)를 제안한다.
SELECT-NEIGHBORS-HEURISTIC(q,C,M,lc,extendCandidates,keepPrunedConnections)
Input: base element q,
candidate elements C,
number of neighbors to return M,
layer number lc,
flag indicating whether or not to extend candidate list extendCandidates,
flag indicating whether or not to add discarded elements keepPrunedConnections
Output: M elements selected by the heuristic
R←∅
W←C // working queue for the candidates
if extendCandidates // extend candidates by their neighbors
for each e∈C
for each eadj∈neighbourhood(e) at layer lc
if eadj∉W
W←W∪eadj
Wd←∅ // queue for the discarded candidates
while │W│>0 and │R│<M
e← extract nearest element from W to q
if e is closer to q compared to any element from R
R←R∪e
else
Wd←Wd∪e
if keepPrunedConnections // add some of the discarded
// connections from Wd
while │Wd│>0 and │R│<M
R←R ∪ extract nearest element from Wd to q
return R
Algorithm 4는 처음 이웃을 구할 땐 가장 가까운 벡터를 선택하지만 다음 벡터부터 이전에 선택한 방향과 다른 벡터들을 탐색하는 것이 특징이다. 아래 예시를 통해 자세히 알아보자.

그림3 처럼 벡터(노란색, q)가 새로 추가될 때 첫 번째 이웃은 가장 가까운 벡터를 선택한다.
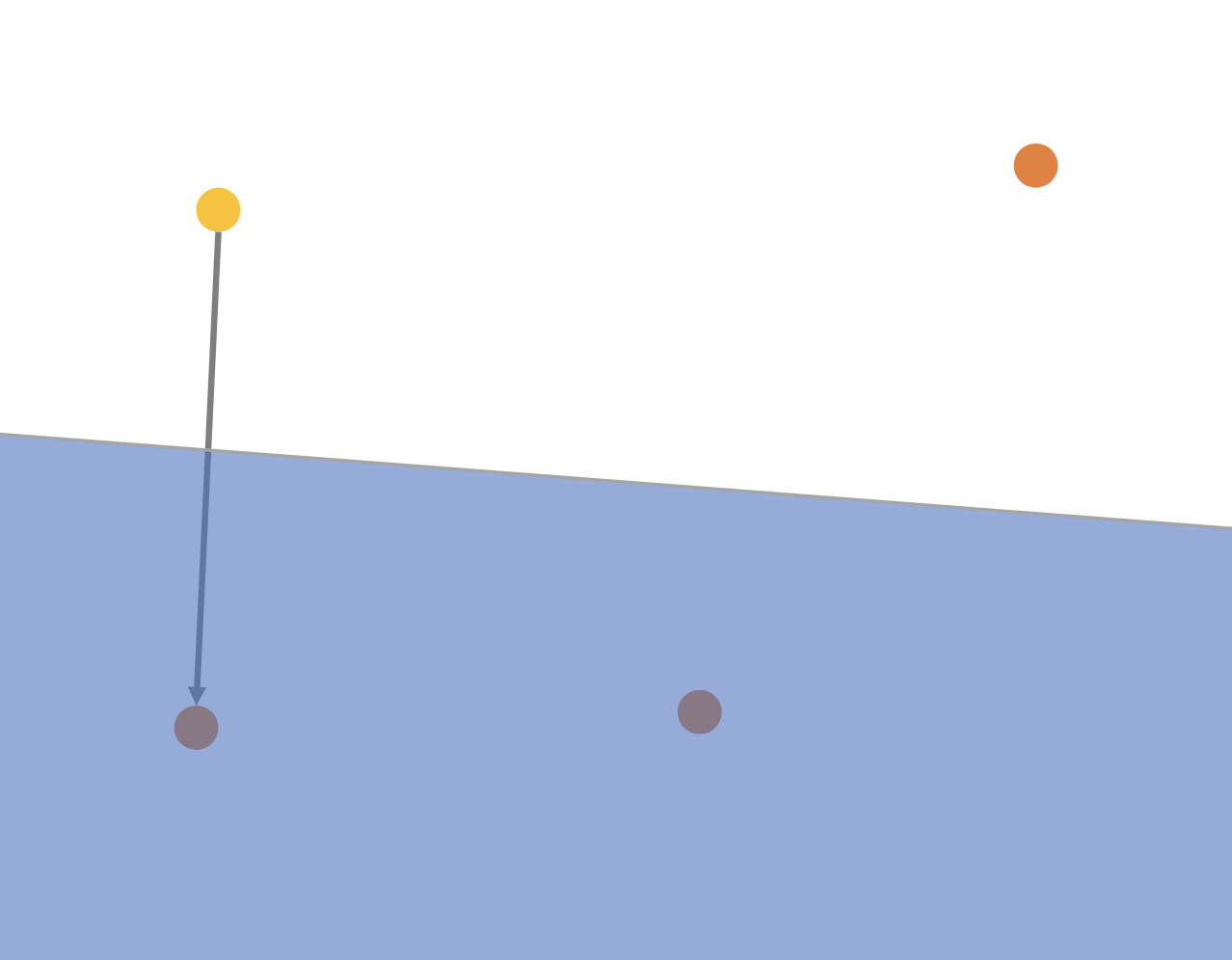
이후 첫 번째 이웃과 직선의 중심에서 수직선을 그어 아래 파란영역에 포함된 벡터들을 모두 후보군에서 제외한다. 만약에 벡터가 3차원 공간이라면 2차원 평면이 기준이 되어 q와 먼 거리의 벡터들을 제외한다. N차원 공간에 대해 N-1차원으로 경계를 만드는 것이다.
(실제 알고리즘과 절차는 약간 다르지만 이 프로세스가 결과를 직관적으로 이해하기 편하다.)
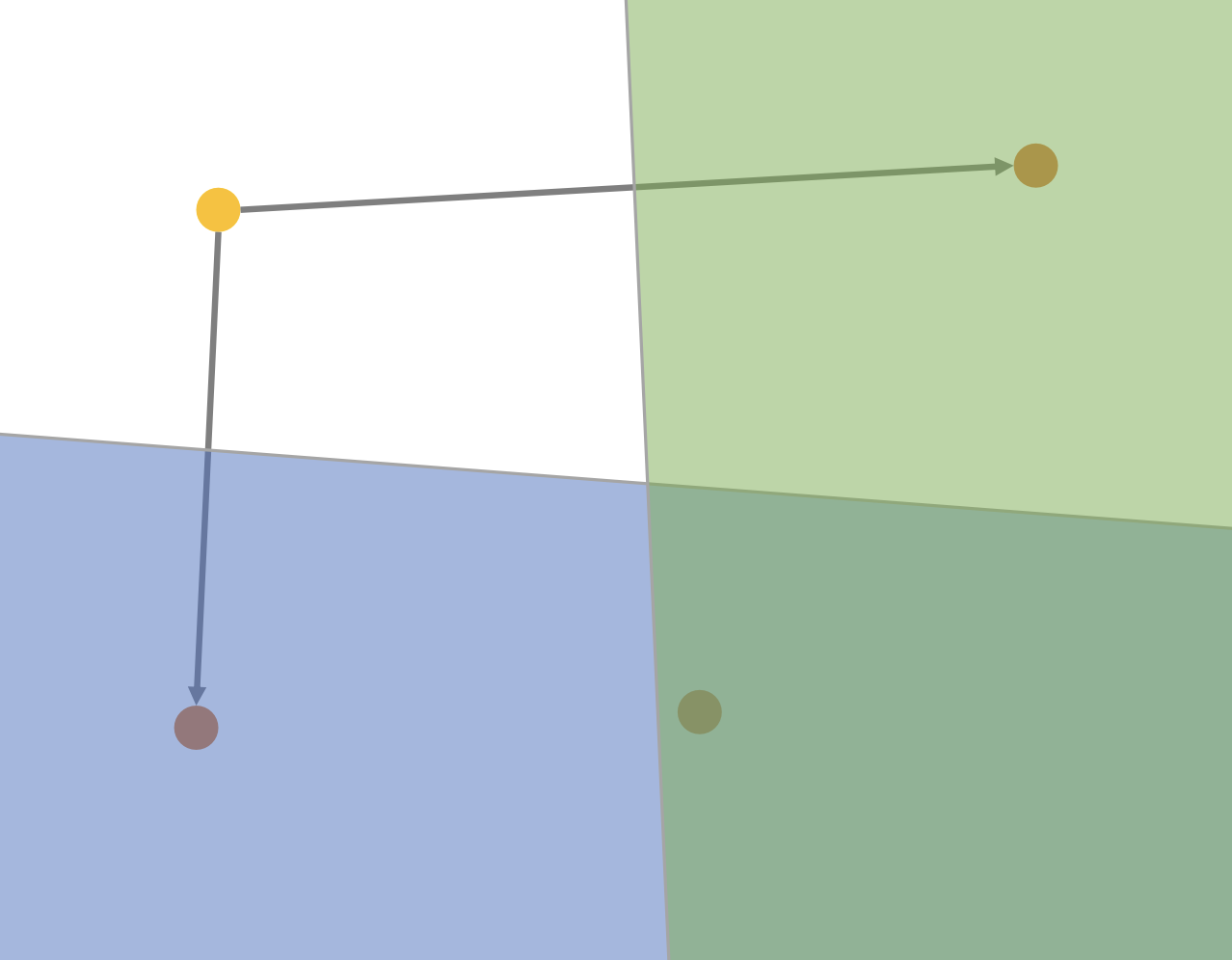
이어서 두 번째 이웃으로 오른쪽위 벡터를 선택하고 마찬가지로 초록색 영역의 벡터들은 후보군에서 제외된다. 이처럼 SELECT-NEIGHBORS-HEURISTIC은 이웃들을 다방면으로 연결하여 그래프 내 강한연결요소(Strongly Connected Component)를 줄인다. (탐색 속도 증가) 또한 군집에서 멀리 떨어진 벡터를 연결하여 탐색 불가능 영역을 최소화 한다. (recall 증가, 논문 Fig. 2. 참고)
2. HNSW
HNSW는 Hierarchical Navigable Small World의 약자로 NSW를 수직 계층적으로 구성하는 것을 뜻한다. 앞서 설명한 NSW를 여러 계층으로 구성하여 탐색 시간을 줄이기 위함이다.
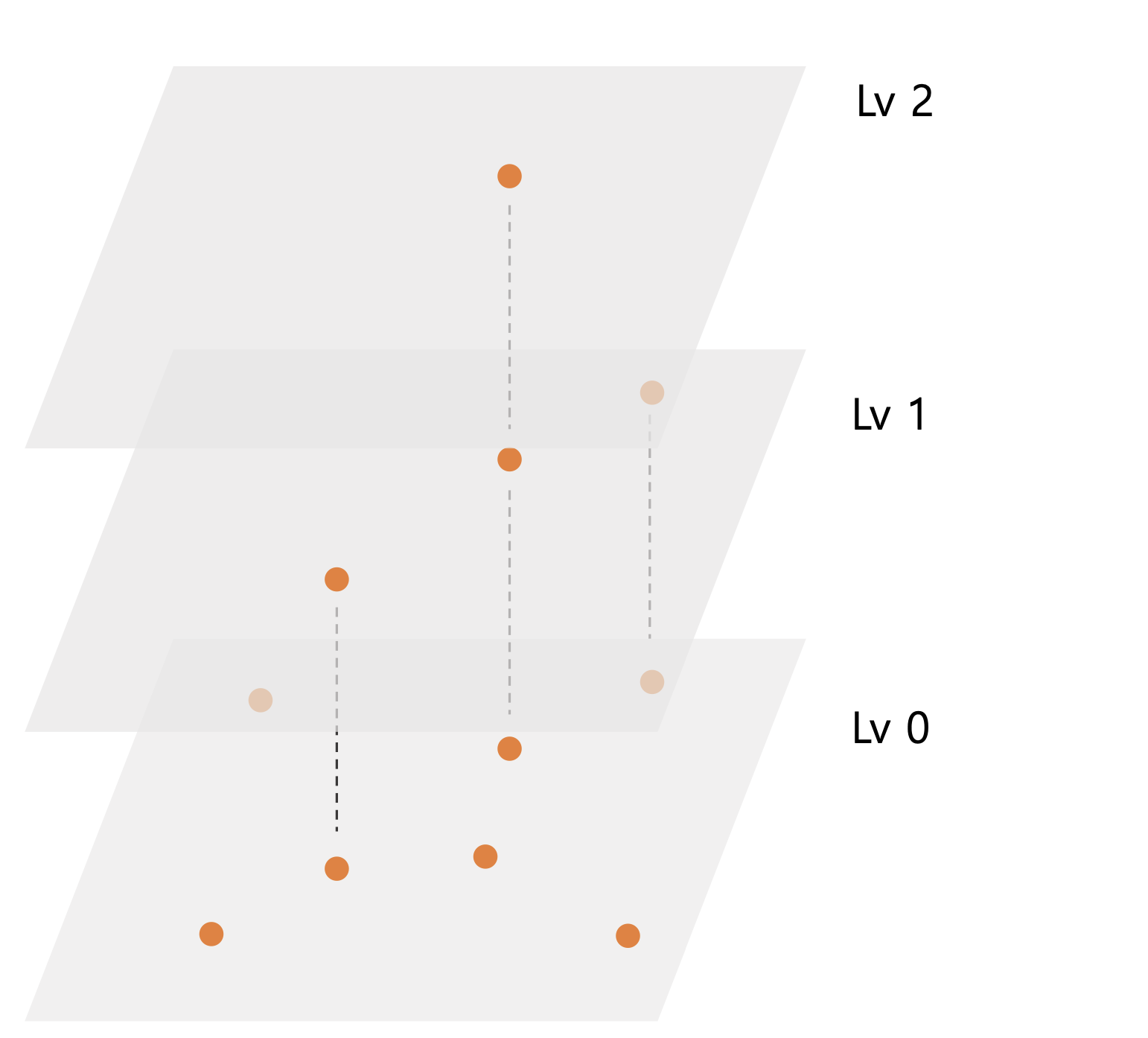
HNSW의 가장 하단 Lv0 에 실제 찾고자 하는 벡터들을 배치한다. 그리고 Len(Lvn)=log(Len(Lvn−1)) 이 되도록 레벨이 높을수록 벡터 수를 log-scale로 줄인다. 이 때 벡터를 선택하는 기준은 랜덤이며 각 Lv의 NSW는 독립적으로 동작한다. 최상위 레벨에는 하나의 벡터만 있으며 이 벡터가 시작 ep(entry point) 이다.
이 계층을 두는 이유는 검색 시 NSW에서 이웃들을 탐색할 때 최적의 시작위치(ep)를 구하기 위함이다. HNSW 논문에 Algorithm 1(색인)과 Algorithm 2(검색) 모두 이 계층을 통해 최적화되어 있으며 두 알고리즘은 유사해 검색 예시 하나로 설명한다.
Algorithm 1 (색인)
INSERT(hnsw,q,M,Mmax,efConstruction,mL)
Input: multilayer graph hnsw,
new element q,
number of established connections M,
maximum number of connections for each element per layer Mmax,
size of the dynamic candidate list efConstruction,
normalization factor for level generation mL
Output: update hnsw inserting element q
W←∅ // list for the currently found nearest elements
ep← get enter point for hnsw
L← level of ep // top layer for hnsw
l← ⌊-ln(unif(0..1))⋅mL⌋ // new element’s level
for lc← L ... l+1
W← SEARCH-LAYER(q,ep,ef=1,lc)
ep← get the nearest element from W to q
for lc← min(L,l)...0
W← SEARCH-LAYER(q,ep,efConstruction,lc)
neighbors← SELECT-NEIGHBORS(q,W,M,lc) // alg. 3 or alg. 4
add bidirectionall connectionts from neighbors to q at layer lc
for each e∈neighbors // shrink connections if needed
eConn← neighbourhood(e) at layer lc
if │eConn│>Mmax // shrink connections of e
// if lc = 0 then Mmax=Mmax0
eNewConn← SELECT-NEIGHBORS(e,eConn,Mmax,lc) // alg. 3 or alg. 4
set neighbourhood(e) at layer lc to eNewConn
ep ← W
if l > L
set enter point for hnsw to q
Algorithm 2 (검색)
SEARCH-LAYER(q,ep,ef,lc)
Input: query element q,
enter points ep,
number of nearest to q elements to return ef,
layer number lc
Output: ef closest neighbors to q
v←ep // set of visited elements
C←ep // set of candidates
W←ep // dynamic list of found nearest neighbors
while │C│>0
c← extract nearest element from C to q
f← get furthest element from W to q
if distance(c,q)>distance(f,q)
break // all elements in W are evaluated
for each e ∈ neighbourhood(c) at layer lc // update C and W
if e ∉ v
v←v∪e
f← get furthest element from W to q
if distance(e,q)<distance(f,q) or │W│<ef
C←C∪e
W←W∪e
if │W│>ef
remove furthest element from W to q
return W
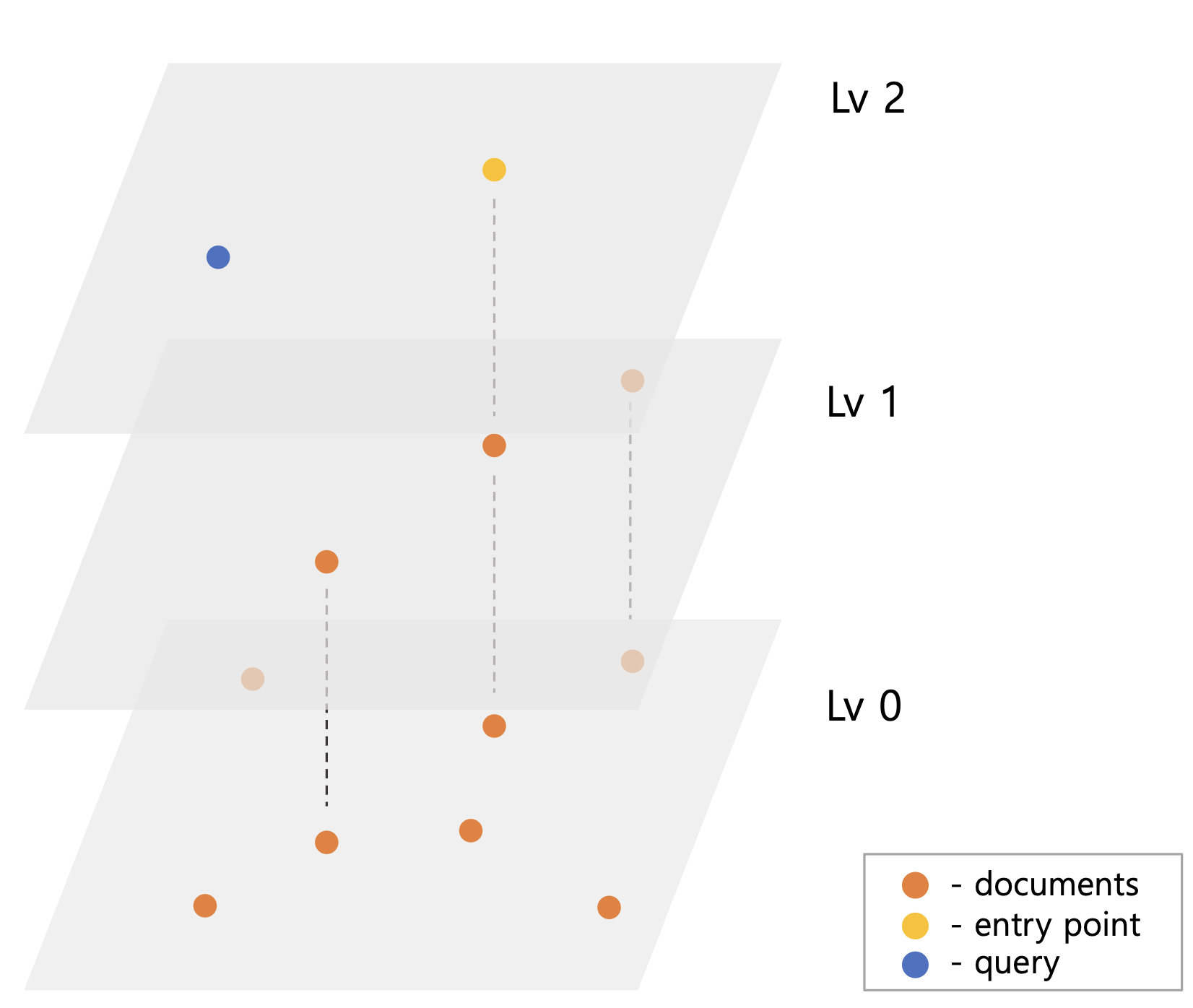
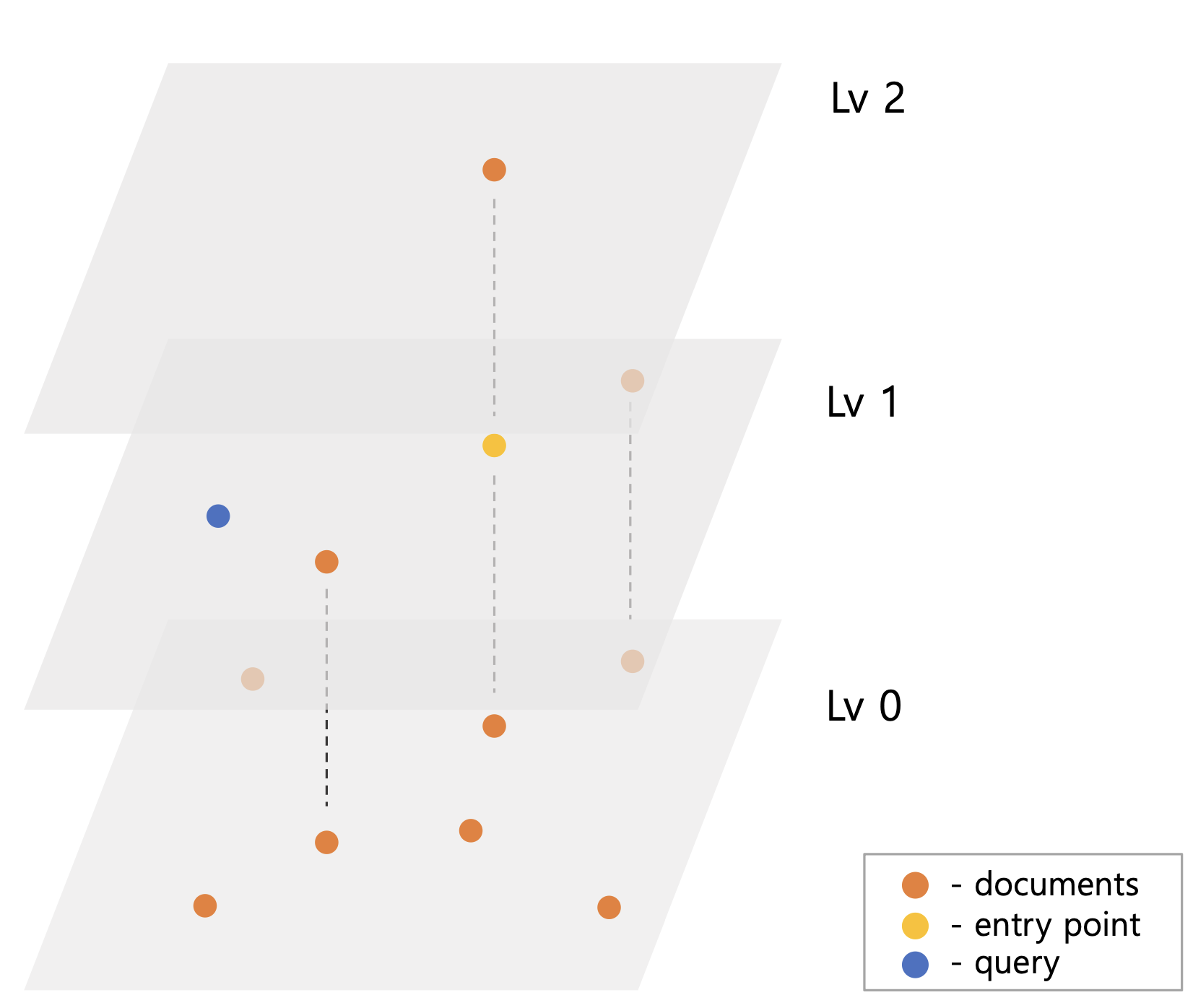
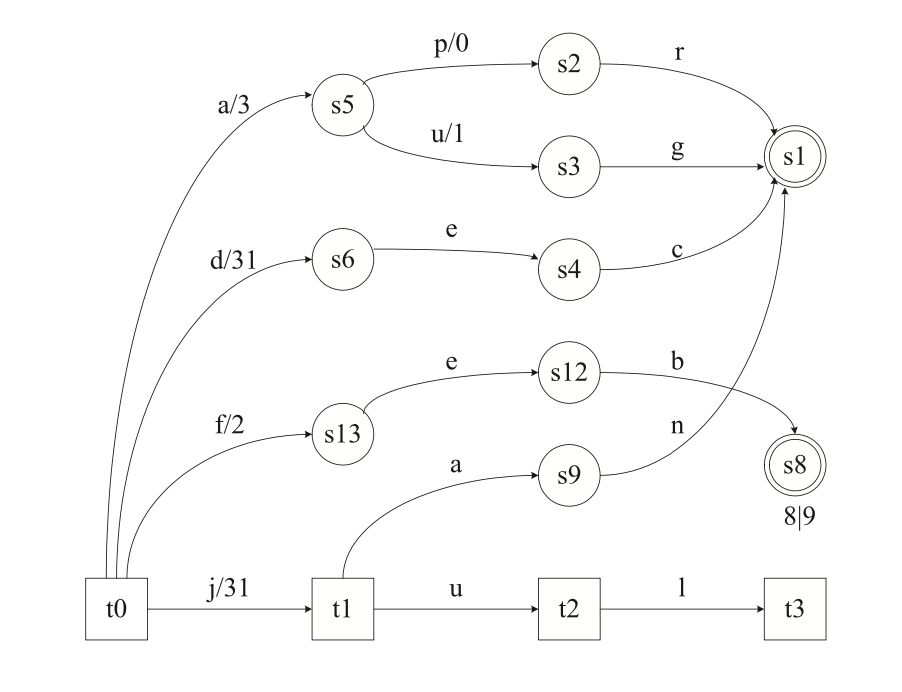
HNSW가 그림5 처럼 색인되어 있고 query 벡터가 들어오면 Lv2의 ep q부터 탐색을 시작한다. Lv2의 ep는 탐색할 이웃이 없기 때문에 동일한 Lv1의 ep에서 탐색을 진행한다. Lv1ep의 이웃들을 탐색하면서 query와 떨어진 거리를 기준으로 priorityQueue에 후보 벡터들을 저장한다. 이는 ef 또는 efConstruction 이라 명명한 후보군 제한 수 설정 때문이다. 그림5 예시와 달리 벡터가 많을 경우 검색 시 모든 벡터들을 탐색할 수 있다. 때문에 ef 수를 넘은 만큼 priorityQueue에서 query와 가장 멀리 벡터들을 제거하여 검색 성능을 높인다.
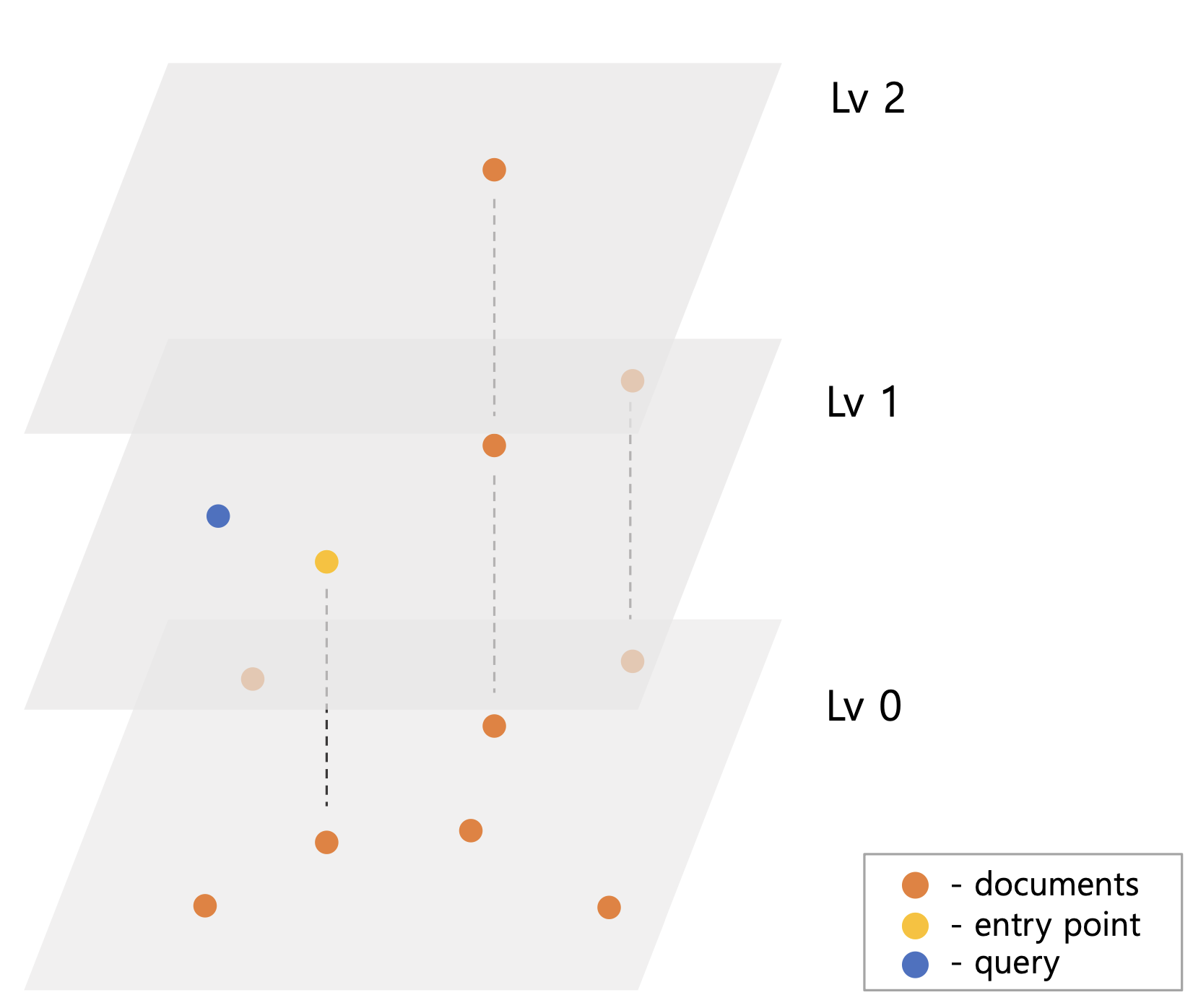
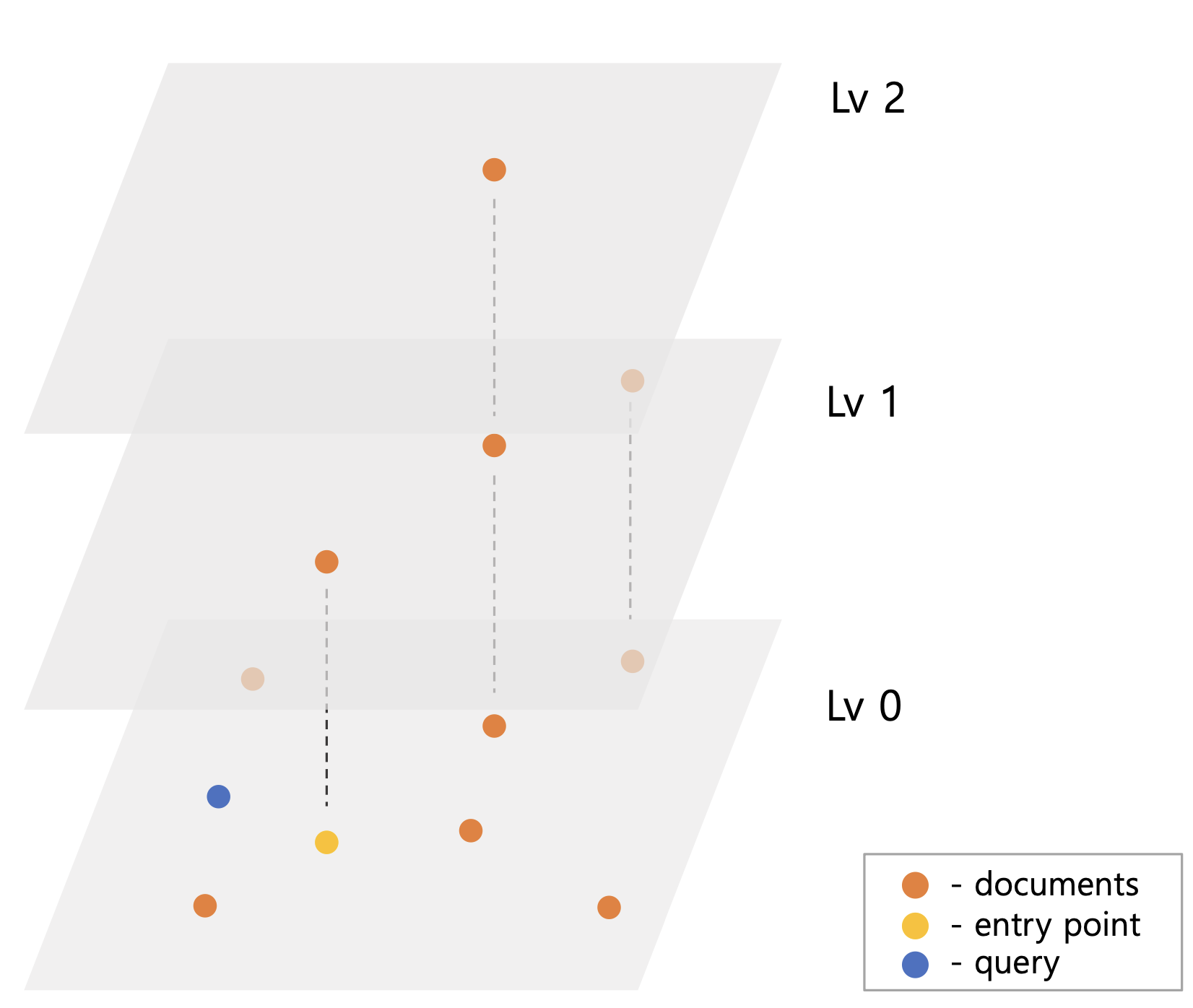
Lv1ep는 그림5-2 처럼 query와 가까운 쪽으로 이동하고 이를 최종 Lv0ep로 한다. 마지막 Lv0 검색은 ep를 결과 priorityQueue에 저장하여 원하는 결과 벡터 수가 나올 때까지 탐색한다.
다음
Lucene9.x에 적용된 HNSW와 개선점
'검색' 카테고리의 다른 글
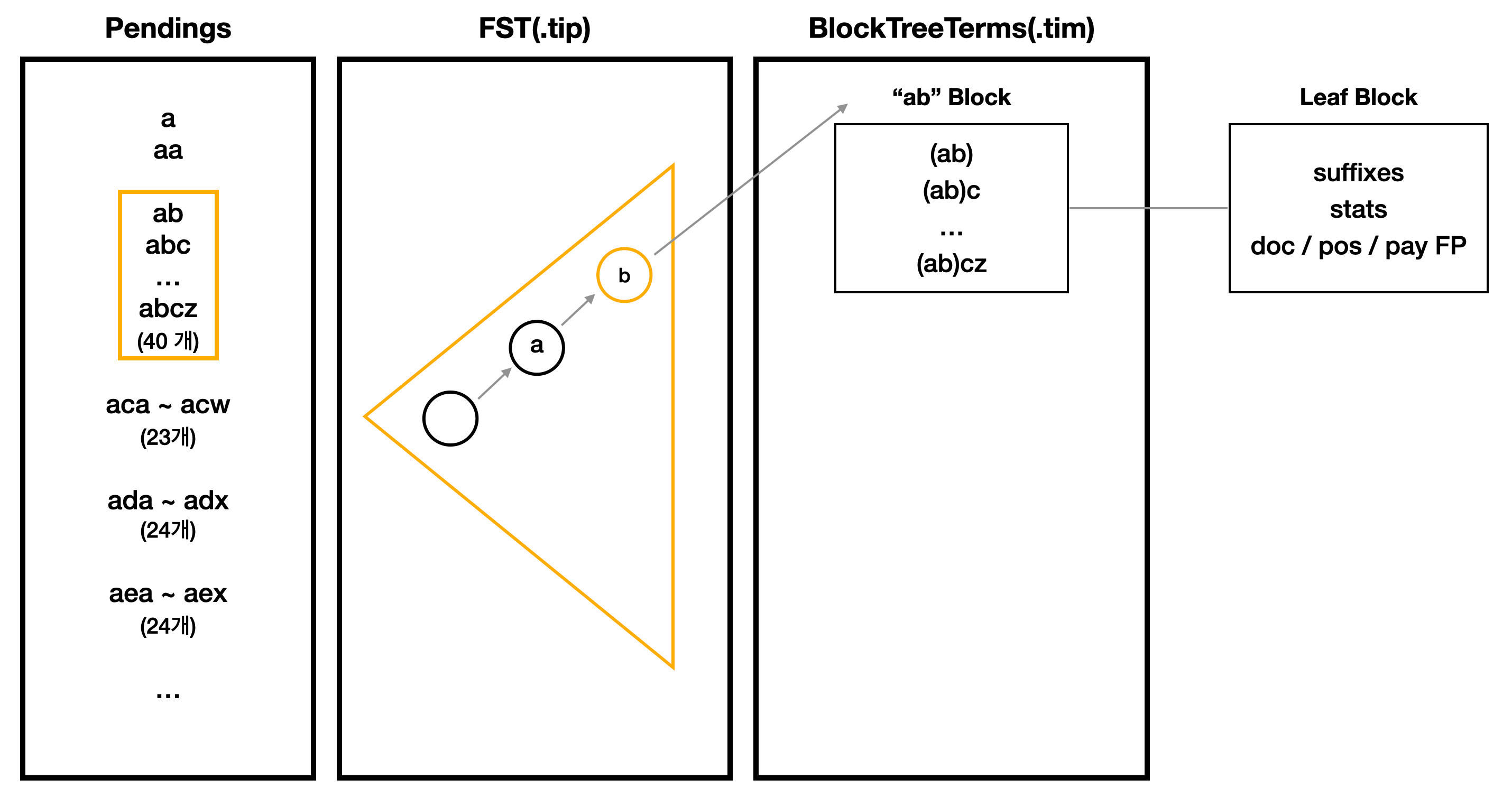
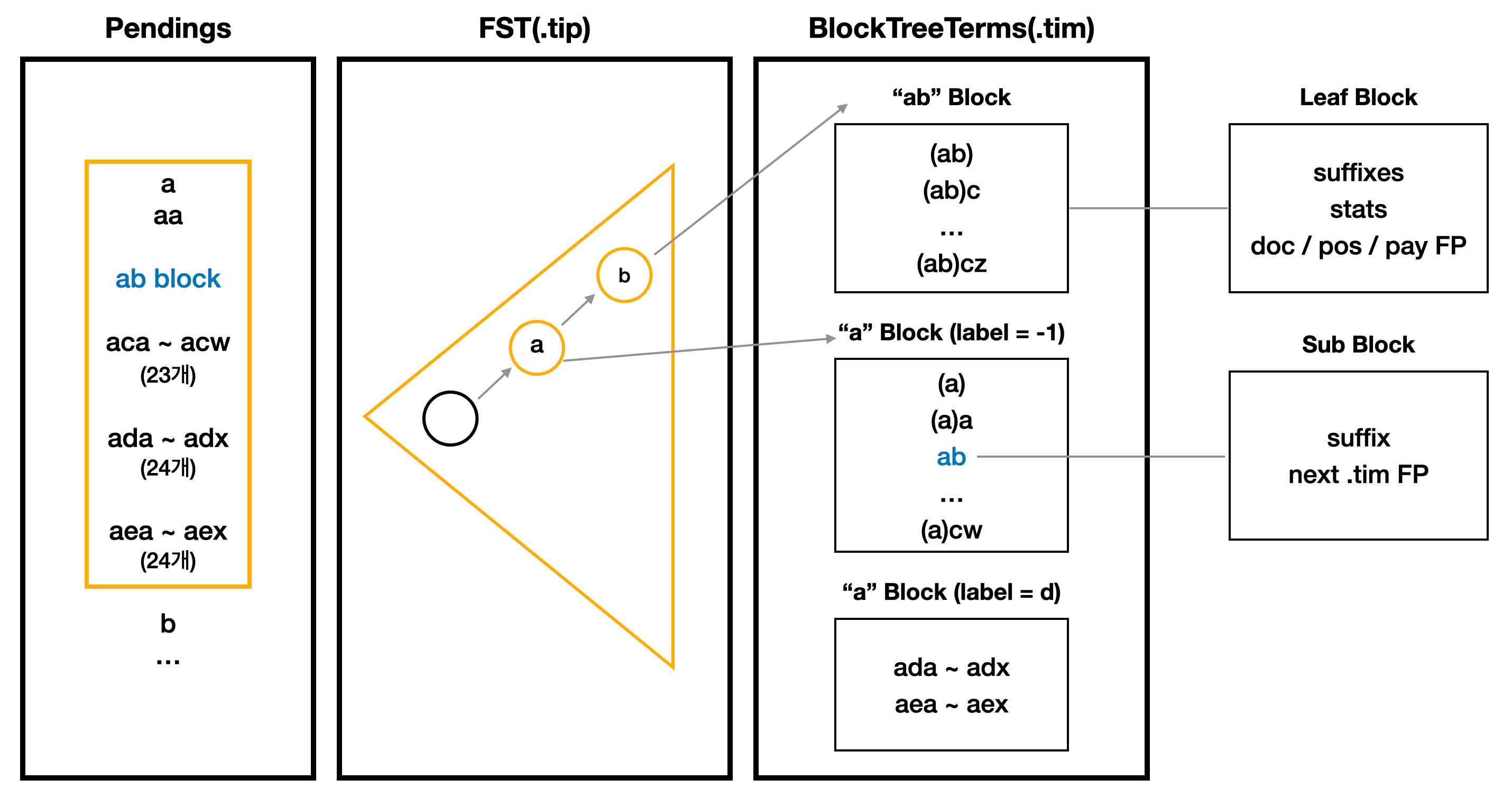
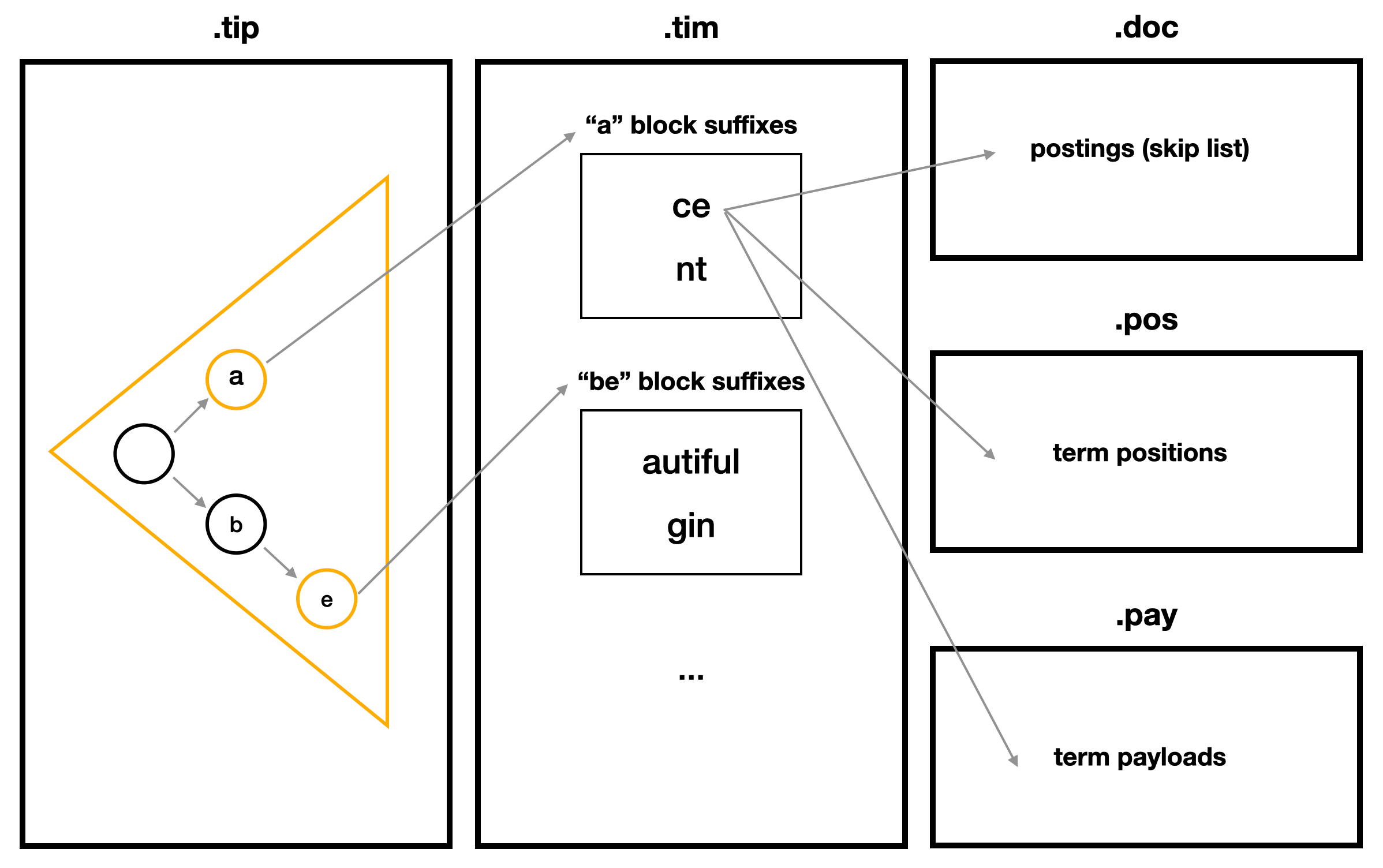
| Lucene 역색인(Inverted Index) 심층분석 3 - BlockTreeTerms (0) | 2023.02.06 |
|---|---|
| Lucene 역색인(Inverted Index) 심층분석 2 - FST (0) | 2023.02.03 |
| Lucene 역색인(Inverted Index) 심층분석 1 - 전체 색인 구조 (2) | 2023.02.01 |